Set-membership Kalman filter and its applications
| Leitung: | Ingo Neumann |
| Team: | Ligang Sun |
| Jahr: | 2017 |
| Förderung: | DFG-Graduiertenkolleg i.c.sens |
| Laufzeit: | 2017 - 2019 |
| Ist abgeschlossen: | ja |
Projektbeschreibung
State estimation is applicable to virtually all areas of engineering and science. Any discipline that is concerned with the mathematical modelling of its systems is a likely candidate for state estimation. Nonlinear filtering can be a difficult and complex subject in the field of state estimation. Developed in the past hundreds years, the stochastic state estimation techniques are most widely applied in the real world. This approach bases on the probabilistic assumptions of the uncertainties in the system, such as Kalman filter and extended Kalman filter, where uncertain parts (usually noise) in the system are assumed to have certain probability distribution(usually Gaussian distribution).
However, in many cases these probability distributions could be questionable, especially when the real process generating the data are complex so that only simplified models can be practically used in the estimation process. There is another interesting approach, referred to set-membership uncertainty state estimation. Developed since 1960s, this approach assumes that the uncertainty is unknown but bounded. No further assumption was made except for its membership of a given bound. This new technique is more appropriate in many cases where the bounded description is more realistic than stochastic distributed hypothesis.
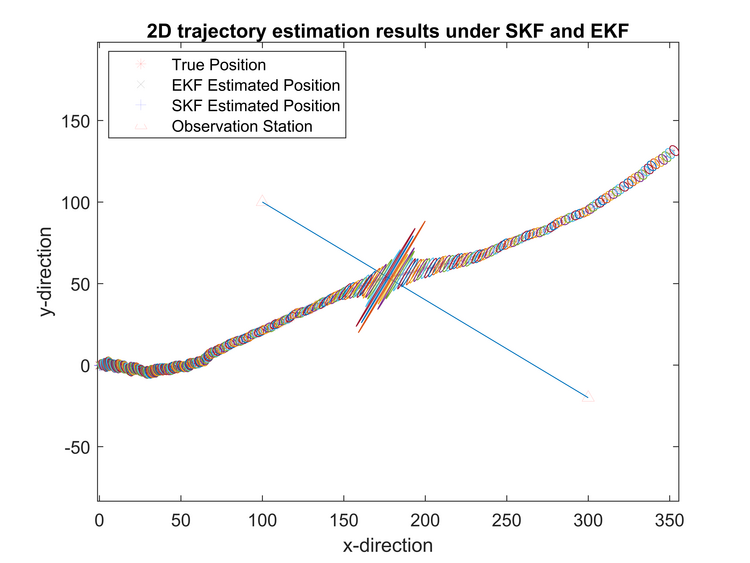
A new filter model called set-membership Kalman (SKF) filter for nonlinear state estimation problems was designed, where both random and unknown but bounded uncertainties were considered simultaneously in the discrete-time system. The main loop of this algorithm includes one prediction step and one correction step with measurement information, and the key part in each loop is to solve an optimization problem. The solution of the optimization problem produces the optimal estimation for the state, which is bounded by ellipsoids. The new filter was applied on a highly nonlinear benchmark example and a two-dimensional trajectory estimation problem, in which the new filter behaved better compared with extended Kalman filter (EKF) results.
Here we use set-membership Kalman filter to estimate the trajectory of one vehicle. As you can see, the output is not a series of single points anymore, there is a series of ellipsoids instead.
The research takes place as part of the GRK i.c.sens.






